Configuración relativamente estática.
La configuración del espacio vectorial en la atmósfera terrestre, orientada
por la densidad del campo magnético polar, parece ser relativamente
estática. El núcleo comprime y alinea solo un segmento del circuito del
campo magnético, formando el eje magnético. Las fuerzas repulsivas del
campo magnético, libres de compresión, se relajan alrededor del eje
comprimido hasta que se equilibran con las fuerzas de atracción.
En este estado aparentemente estático, las fuerzas de atracción consisten en
aumentar la densidad del espacio vectorial orientado, alcanzando su máximo
en el eje magnético. Así, se establece una jerarquía estática de la densidad
del espacio vectorial orientado, una configuración característica de las
estructuras vectoriales macroscópicas. En esta configuración, el espacio
vectorial orientado no se mueve hacia el centro, sino que se compone de
estructuras vectoriales, estáticas o dinámicas. Estas interacciones fueron
interpretadas por Aristóteles, Arquímedes y otros. Aristóteles explicó por
qué algunos cuerpos caen y otros ascienden al cielo, y Arquímedes explicó
por qué algunos cuerpos se hunden en el agua y otros flotan. Nadie explica
por qué los aviones pueden volar. Obviamente, la configuración del espacio
vectorial, al ser reciente, está ausente en la cultura de la civilización.
En la cultura de la civilización se considera que la Tierra fue creada por
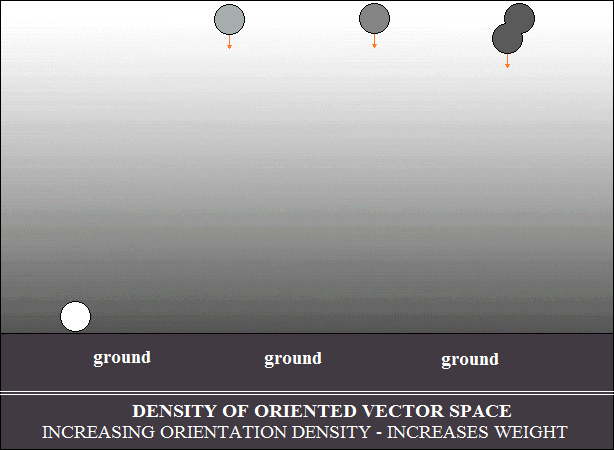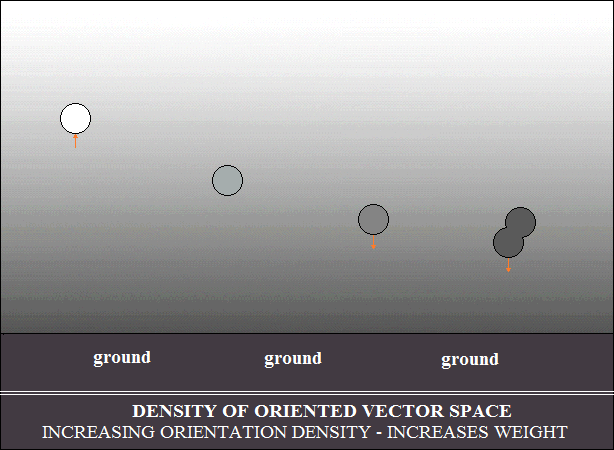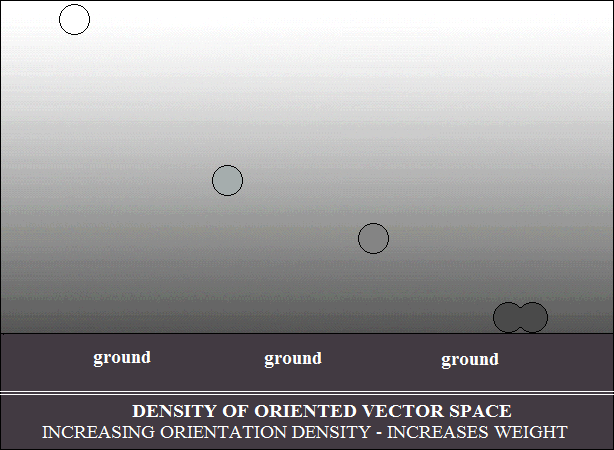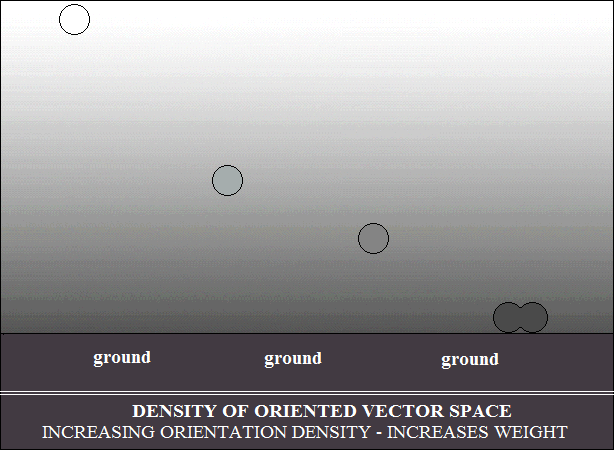
Dios, o como dijo Georges Lemaitre, por el Big Bang. El primer dibujo
muestra cómo la densidad de orientación del espacio vectorial justifica el
razonamiento de Aristóteles y la ley de Arquímedes. El segundo dibujo
muestra la composición vectorial de la velocidad de movimiento de los
objetos, con la densidad de orientación del espacio vectorial en el que se
mueven. La velocidad de movimiento orienta el espacio vectorial en la
dirección y sentido del movimiento. Al ser la orientación paralela, las
fuerzas repulsivas reducen la densidad de orientación del espacio vectorial.
Por lo tanto, el objeto se ve rodeado por una disminución
de la densidad del espacio vectorial, es decir, de su peso.